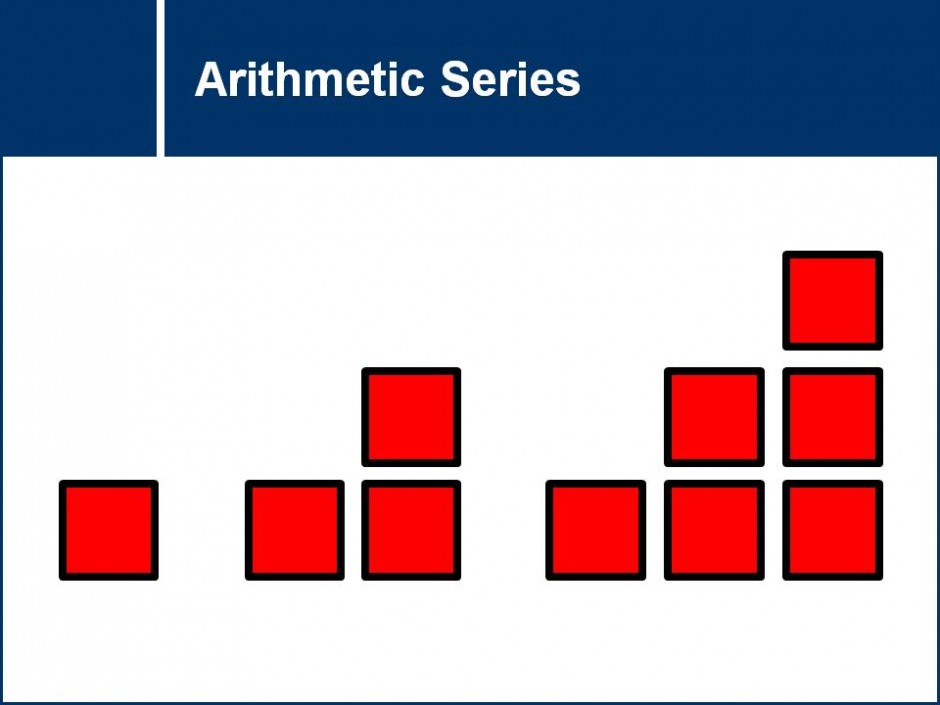
This question set introduces the concept of arithmetic sequences and their properties. Students will be tested on their ability to recognize patterns and think critically to derive general formulas. 
common difference, common ratio, math 11-12, patterns, sequences, series
(2 votes, average: 3.50 out of 5)
Loading...
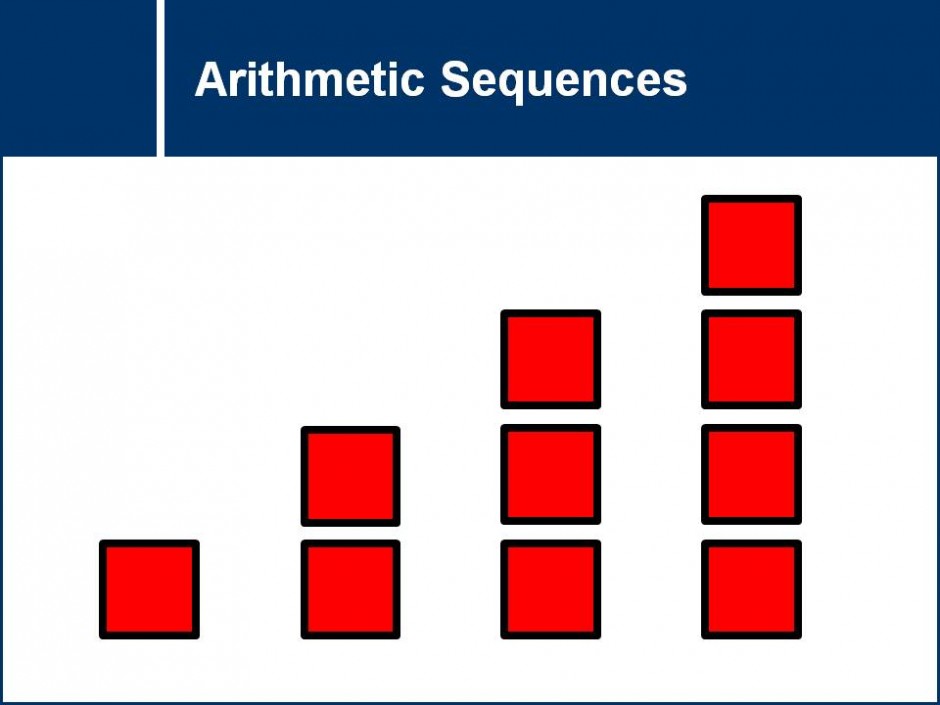
How can the sum of all the numbers between 1 and 100 be found quickly? This question set covers ways to solve this problem as well as finding the sum of more complex arithmetic series.
arithmetic series, common ratio, log laws, math 11-12, patterns, proof, sequences, series, sum of series, sums
(1 votes, average: 5.00 out of 5)Loading...
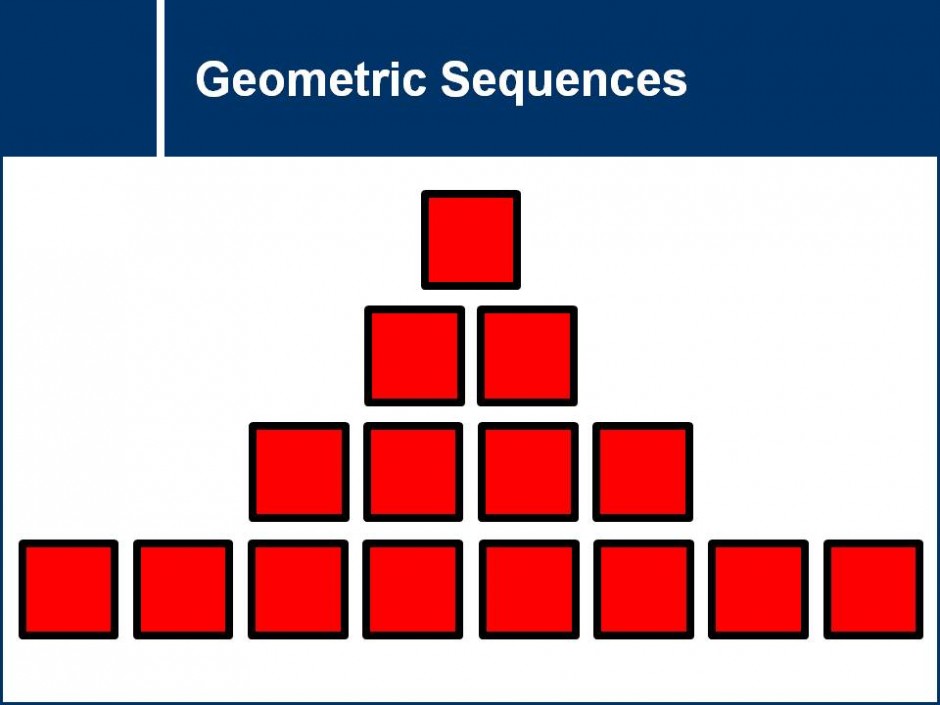
Consider a sequence of numbers where the next number is always twice as larger as the previous. This question set reveals how the nth term of a geometric sequence can be found, where consecutive terms in the sequence are always in the same ratio.
common ratio, exponents, geometric, patterns, powers, sequences, series
(1 votes, average: 5.00 out of 5)Loading...
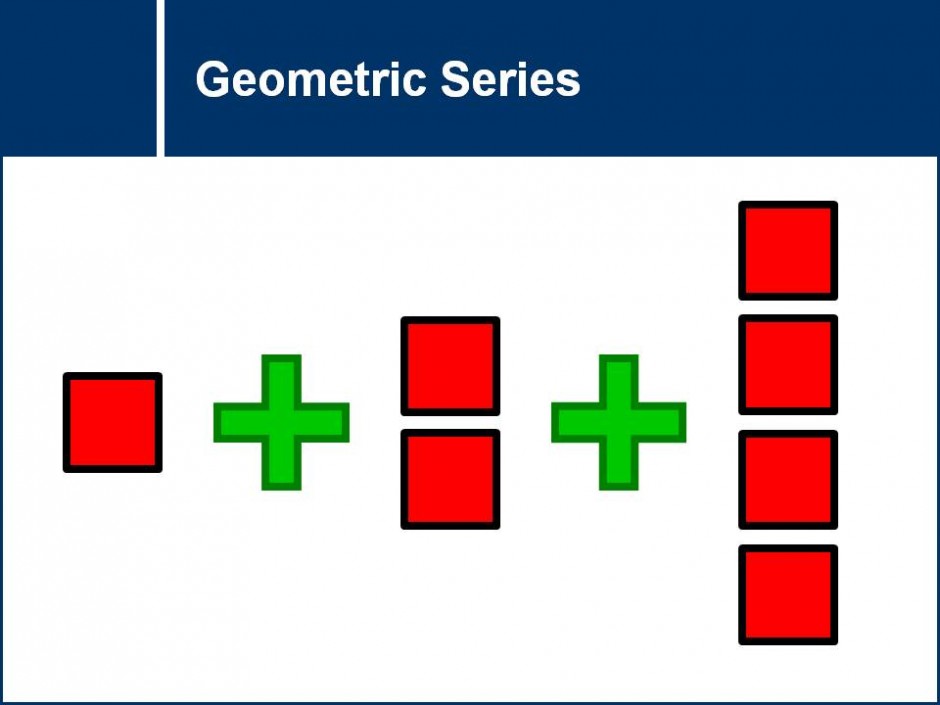
A general formula to find the sum of the first n terms of a geometric series is discovered. The properties of this formula will then be tested in the following questions.
common ratio, exponents, geometric series, math 11-12, patterns, percentages, proof, ratios, sequences, series, sum of series
(2 votes, average: 5.00 out of 5)Loading...
